Leetcode-Array-189.轮转数组

发表于 更新于 分类于 ， 阅读次数： 本文字数： 630 阅读时长 ≈ 2 分钟

https://leetcode.cn/problems/rotate-array/description/?envType=study-plan-v2&envId=top-interview-150

思路

主要有以下几种思路，因为我曾经在清华邓公数据结构网课中听到过，所以很快直接想到了最佳算法。

  1. 每次移动一位，将整个数组移动 次，因为 ，所以可以将时间复杂度近似为 ，空间复杂度为

  2. 直接将一个元素移动 位，到对应的位置上，但是注意，我们需要暂存下被挤占位置的元素的值，但是这个被挤占了的并不是下次就能被用到，所以实际上需要的额外空间接近于 ，时间复杂度为

  3. 区间逆转，我们能不能在思路2的基础上进行优化，想办法对数组进行处理，使得每次被挤占的元素正好是下次要用到的元素？进一步的，我们能不能预处理之后，让 与 ，直接交换位置就可以？确实存在这样的解法：

    1. 首先将 这前半长度为 的区域倒置。

    2. 然后将 这后半长度为 的区域进行倒置。

    3. 最后将整个数组进行倒置，神奇的发现，这样的结果与轮转 次的结果是一致的。我们用下面这个图来说明：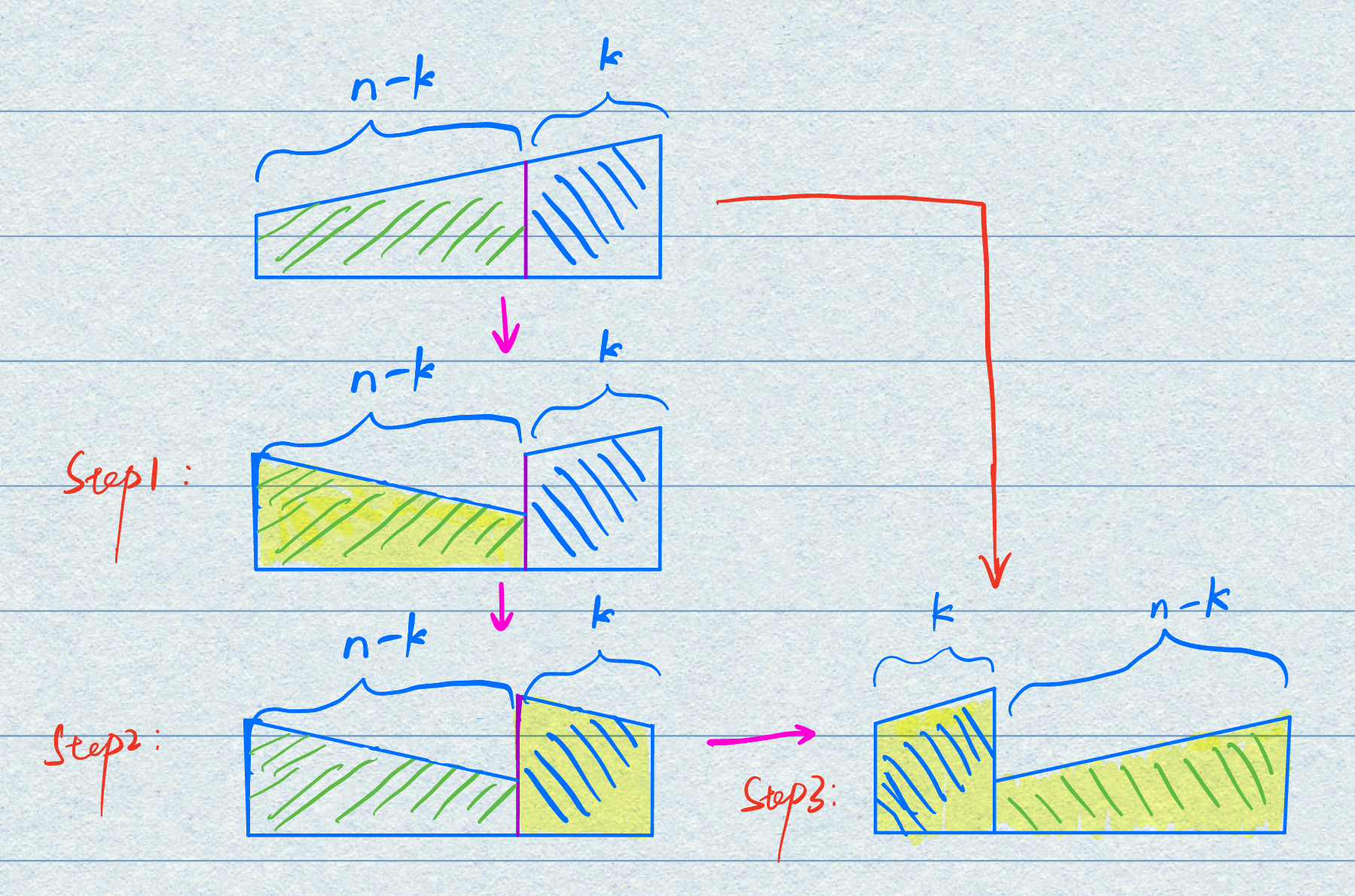

      轮转数组（黄色部分表示相对于上一步的变化，红色箭头表示轮转K步，桃红色箭头表示算法的三个步骤）

代码

代码很简单，就不需要伪代码了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    // 思路1：顺序移位，nk 复杂度，其中 k=k%n,所以约等于 n^2
    // 思路2：直接将一个元素移到对应的位置上，但是似乎存在一个问题，对应的两个位置并不能直接交换，所以不可行
    // 思路3：有没有办法进行一个预处理，使得预处理后的数组上 做一次颠倒就可以？有，首先将 n-k 部分进行颠倒，然后将后k部分颠倒，这是预处理，之后将整个数组颠倒。

    public void reverse(int[] nums,int i,int j){
        int tmp=0;
        while (i<j){
            tmp=nums[i];
            nums[i]=nums[j];
            nums[j]=tmp;
            i++;
            j--;
        }
    }
    public void rotate(int[] nums, int k) {
        int len =nums.length;
        k%= len;
        reverse(nums, 0,len-k-1);
        reverse(nums,len-k,len-1);
        reverse(nums,0,len-1);
    }
}